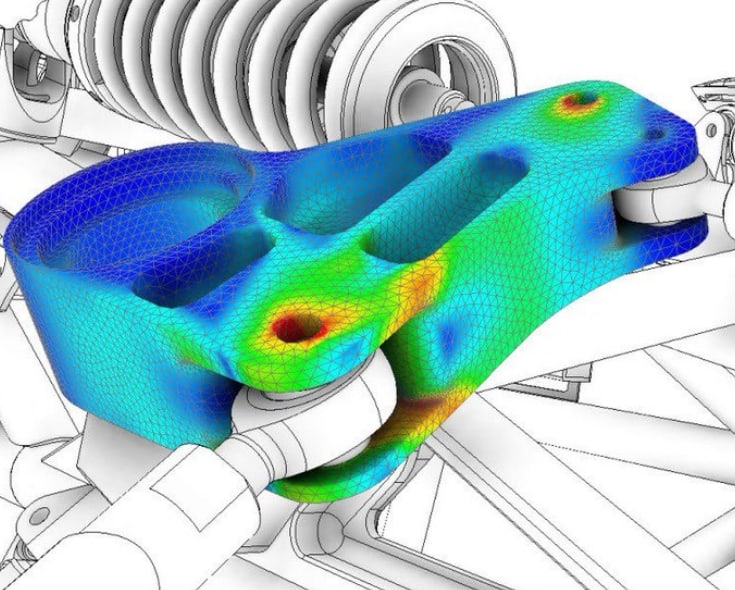
In the previous section of this series, we discussed the following topics:
- Part 1 – Allowable Design Practices.
- Part 2 – Material Classification Practices.
- Part 3 – Mechanical Stress Terminology.
Above are a few foundational pieces for finite element analysis (FEA), stress analysis, and structural analysis. You can get an analytical solution and FEA analysis results without having a design allowable, material properties, or knowing the material classification. However, you won’t know what the result means without having the stress and strain curve information. Or if you take the time to set up each material with its Stress Allowable.
Static Failure Theories (Ductile Materials)
All failure theories are material, load, and temperature-dependent. We need to be aware of the ductile-brittle transition temperature if we expect to encounter extreme temperatures. This post will cover the failure theories of Maximum Shear Stress and Distortion Energy. Other material failures, brittle material, plastic deformation, and buckling will be covered in the future.
Maximum Shear Stress Theory (MSS):
Maximum Shear Stress Theory predicts that failure will occur when the maximum shear stress in a uniaxial tension test exceeds the material’s shear strength. Yielding begins when the maximum shear stress exceeds the allowable stress in an element, exceeding the maximum shear strain values obtained from tensile tests of materials of the same material type.
\tau_{max} = \frac{\sigma_{1} + \sigma_{3}}{2} = \frac{S_{y}}{2}Any stress theory can be plotted and will develop an envelope. The inside area of that envelope is where failure will not occur, leading to a safe design.
MSS is commonly used during the design process and is well-accepted, but we find it could be more accurate. For example, the figure below shows that the failure occurs after MSS predicts it will, leading to an increase in the safety factor, which we might view as a good outcome early in the design process when there are many unknowns.
However, during the validation stage of any project, it is not desirable to use MSS as there is a chance that MSS will increase cost needlessly.
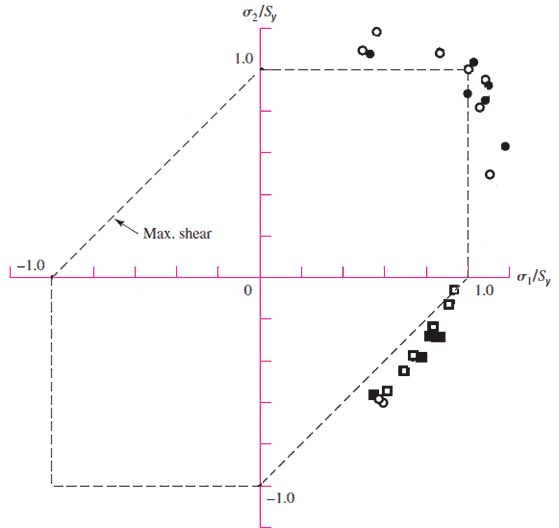
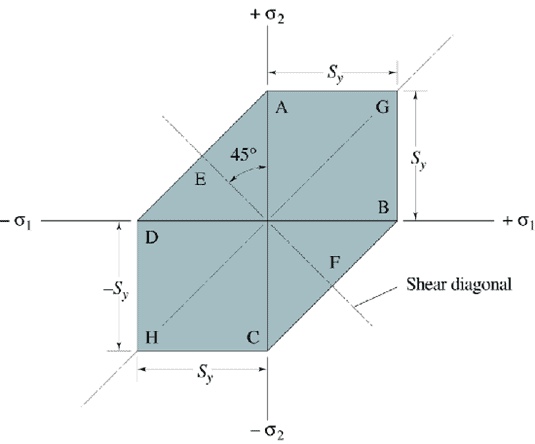
Additionally, the Maximum Shear Stress Theory for Ductile Materials is also known as the Tresca Theory. A factor of safety (n) can be set or determined using the following formula:
n=\frac{S_{y}}{\sigma_{1} - \sigma_{3}}Distortion Energy Theory (von Mises yield criterion)
The distortion-energy theory is the most widely used theory for ductile materials. The Distortion Energy Theory predicts that material will yield when the strain energy per unit volume reaches or exceeds the yield strain energy per unit volume for simple tension or compression.
The theory was developed by observing that ductile materials stressed hydrostatically under deep water exhibited greater yield strengths than previously obtained at atmospheric pressure.
The Distortion Energy Theory argues that if you divide strain energy into hydrostatic volume changing energy and angular distortion energy, yielding is primarily affected by the angular distortion energy, causing your model to yield. Below is some point of interest:
- It is a scalar, unsigned stress quantity resulting in no direction or indication of tension or compression, resulting in an always positive value with no direction.
- Allows Multiaxial Stress States To Be Compared To Failure Criteria Obtained From A Uniaxial Tension Test (this is very important)
- Only Considers Strain That Produces Distortion (Shape Change)
- Only the stresses which act to distort the shape of the part will matter when checking for yield.
When plotted, The Distortion Energy Theory develops an envelope, and the interior area of that envelope is considered an area where failure will not occur. Leads to a safe design
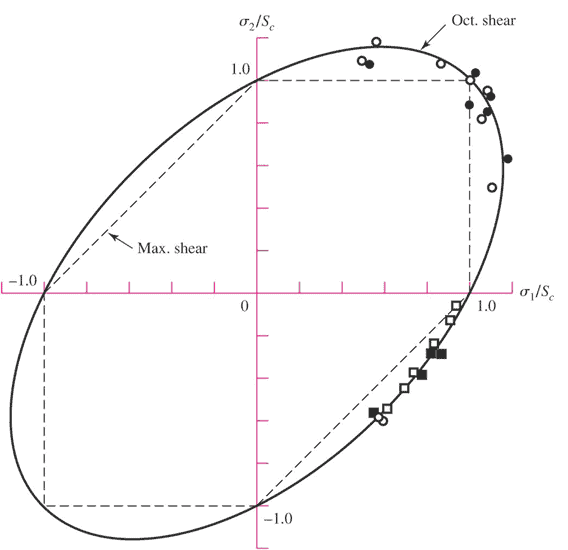
The distortion-energy theory has many names:
- von Mises theory
- von Mises–Hencky’s theory
- The shear-energy theory
- The octahedral-shear-stress theory
Yield begins when the maximum shear stress in a stressed material exceeds the maximum shear stress in a specimen of the same material when that specimen starts to yield.
\sigma_{e} = \frac{\sqrt{2}}{2}\sqrt{(\sigma_2-\sigma_1)^2+(\sigma_3-\sigma_1)^2+(\sigma_3-\sigma_2)^2}Distortion Energy Theory is commonly used for analysis situations, but when employed with sound safety factors, Distortion Energy Theory is completely appropriate for design applications. And, for design and analysis purposes, a factor of safety (n) can be set or determined using the following equation:
\sigma_e=\frac{S_y}{n}The Maximum Normal Stress Theory:
Maximum Normal Stress Theory is the oldest of the failure theories, and most text states that maximum normal stress is not suitable for predicting ductile fracture and failures. The theory shows that failure will always occur whenever the greatest tensile or compressive stress exceeds the uniaxial tensile or compressive strength. And, testing data shows that it correlates best with brittle material.
As we have shown in an early post, There are three mutually perpendicular planes passing through any given point in a body such that the stresses on each are purely normal, either tension or compression.
\sigma_{min,max} = \frac{\sigma_1+\sigma_3}{2} \pm \sqrt{\frac{\sigma_1 - \sigma_3}{2}+\tau_{1,3}^2}However, a brittle material will fail when the maximum principal stress exceeds some value, independent of whether other stress tensor components are present. Experiments in uniaxial tension and torsion have corroborated this assumption. Still, the failure envelope clearly shows that the maximum normal stress theory is only valid in the first and third quadrants. It does not account for the interdependence of normal and shear stresses, which affects the second and fourth quadrants.
Final Thoughts
FEA simulation is a great tool for engineers to investigate structural designs, but you have to know what the results mean. There are two theories on what initiates ductile material to fracture: the distortion energy theory and the maximum shear stress theory.
Ultimately, these theories appear to predict failure in structures when the shear stress exceeds a certain limit. However, the distortion energy theory appears to be more accurate with the initial conditions (material properties and geometric properties) than we used in FEA structural analysis.
It seems as though the Von-Mises stress criterion is most closely approximated by material constants and geometric properties(cross-sections). The Max-stress criterion tends to over-predict failure, especially near yield.
Although the Finite Element Method (FEM) is a great tool for engineers to investigate structural designs, you must know what the results mean to be effective.