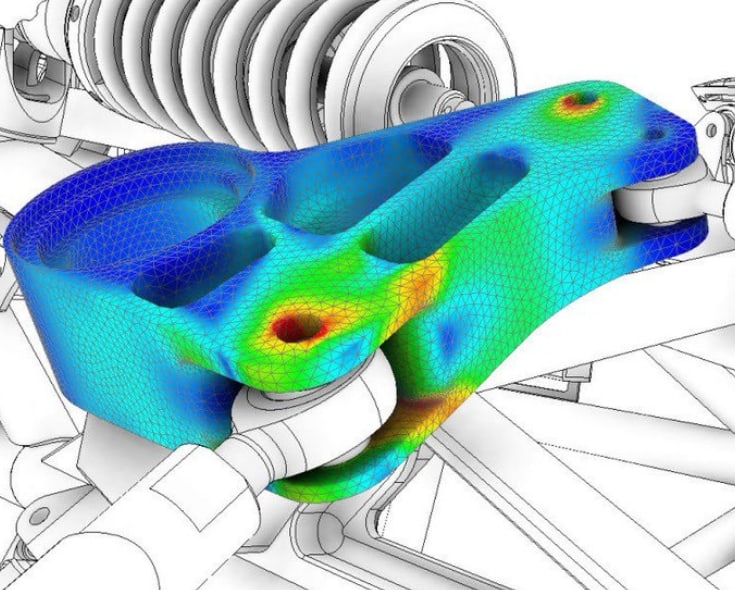
In this latest section of the series, we’re going to continue our in-depth discussion of structural mechanics and stress analysis by covering brittle materials failure analysis theory and mechanical stress terminology.
In the previous section of this series, we discussed the following topics:
- Part 1 – Allowable Design Practices.
- Part 2 – Material Classification Practices.
- Part 3 – Applied Engineering Failure Analysis Theory and Mechanical Stress Terminology.
- Part 4 – Static Failure Theories (Ductile Materials)
- Maximum Shear Stress Theory (MSS)
- Distortion Energy Theory (von Mises yield criterion)
- The Maximum Normal Stress Theory
Static failure analysis of brittle materials is interesting because not all materials have compressive strengths equal to their corresponding tensile values. For example, the yield strength of some alloys in tension may be as little as 50% of their corresponding values in compression.
The ultimate compressive strength of some cast iron varies greatly from the ultimate tensile strength. Therefore, when studying the failure of brittle materials, it is important to consider those theories.
In this post, we will learn about Maximum Normal Stress Theory, Coulomb–Mohr (C–M), and its applications to FEA analysis and analyzing brittle material failure modes
The Maximum Normal Stress Theory:
Modern texts state that the Maximum Normal Stress Theory (MNS) is unsuitable for predicting ductile failures. MNS shows that failure always occurs whenever the greatest compressive or tensile stress exceeds a material’s uniaxial compressive or tensile strength. And testing data shows that it correlates best with brittle materials.
As we showed in a previous post, at any given point on a body, three mutually perpendicular planes pass through it. The stresses on each are purely normal, either tension or compression.
The MNS theory states that failure occurs whenever one of the three principal stresses equals or exceeds the strength.
\sigma_1\geq \sigma_2\geq\sigma_3
MNS theory predicts that failure occurs whenever:
\sigma_1\geq S_{ut} \:\text{or}\: \sigma_3 \leq -S_{uc}Where Sut is the ultimate tensile strength, and Suc is the ultimate compressive strength given as positive quantities.
For uniaxial loading conditions, the principal stress must be calculated with these loadings. According to the maximum normal stress failure theory, the biggest principal stress is responsible for the material’s failure. Once the biggest principal stress reaches the material’s ultimate failure stress, brittle fracture occurs.
\sigma_{min,max} = \frac{\sigma_1 + \sigma_3a} {2}\pm\sqrt{\frac{\sigma_1 + \sigma_3}{2}+ \tau^2_{1,3}}However, brittle materials fail when the maximum principal stress exceeds some value. Experiments in uniaxial tension and torsion have corroborated this assumption. But the failure envelope clearly shows that the maximum normal stress theory is only valid in the 1st and 4th quadrants, not the 2nd and 3rd quadrants. It does not account for the interdependence of normal and shear stresses, affecting the 2nd and 3rd quadrants.
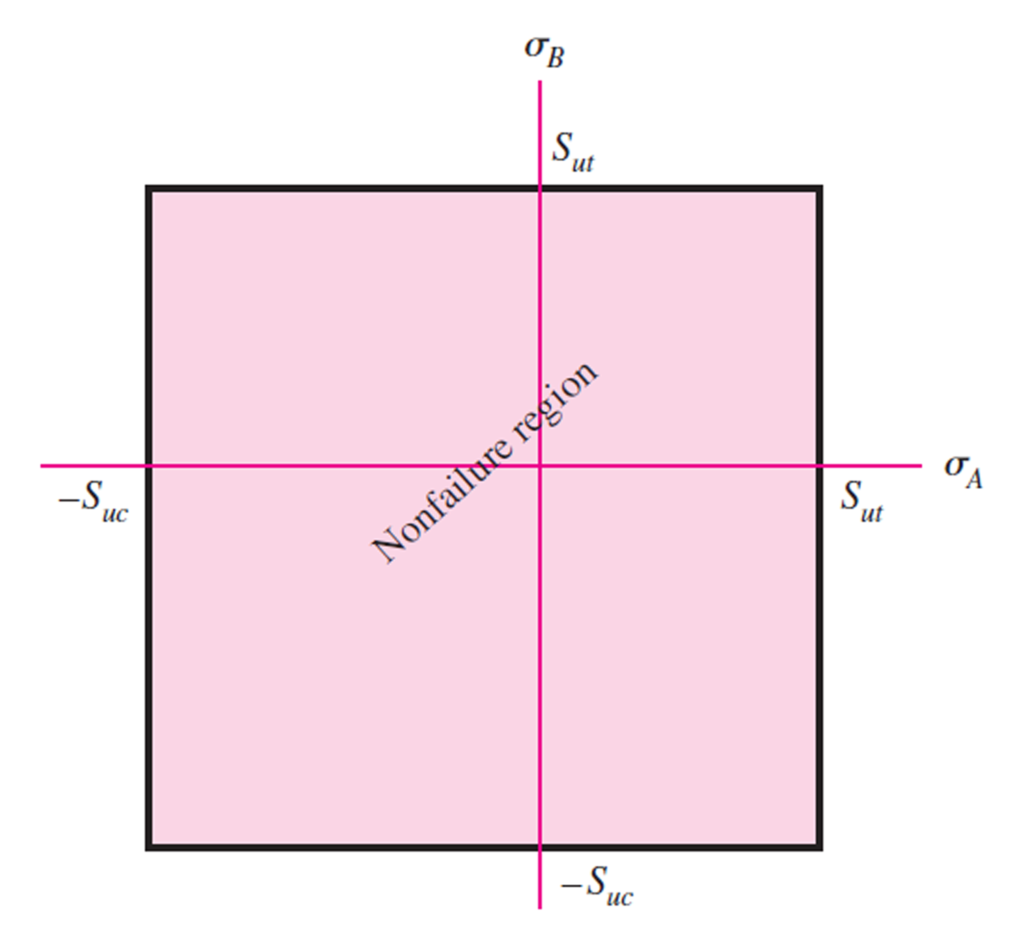
Mohr-Coulomb Theory
Mohr-Coulomb theory is a theory that describes the response of brittle materials to shear stress and normal stress. It was first presented in 1908 by Mohr and further developed by Siegmund von Coulomb in 1922.
This theory applies to materials with high compressive and low tensile strength. Plastic deformation is assumed to occur when a catastrophic failure occurs. In mechanical engineering, Coulomb’s internal friction hypothesis is used to determine the combination of shear and normal stress that will cause a fracture in a material.
The Mohrs circle determines which principal stresses will produce this combination of shear and normal stress. The principle of normality states that the stress introduced at failure will be perpendicular to the line describing the condition for a fracture.
The fracture occurs when the maximum and minimum principal stresses at any given point combine for a condition that meets or exceeds the theory equation:
- Failure Occurs When Mohr’s Circle At A Point In The Body Exceeds The Envelope Created By The Two Mohr’s Circles For Uniaxial Tensile Strength And Uniaxial Compressive Strength.
- Brittle Materials Fracture, There Is No Yielding.
Failure lines are a function of tensile and compressive strengths. Shear strength is a function of these
S_{sy}=\frac{S_{yt}S_{yc}}{S_{yt}+S_{yc}}- Brittle Fracture In Tension Is Considered Due To Normal Tensile Stress Alone, And Thus The Maximum Normal-stress Theory Is Applicable.
- Brittle Fracture In Compression Is Due To Some Combination Of Normal Compressive Stress And Shear Stress.
Must Order Principal Stresses
\sigma_1\geq \sigma_2\geq \sigma_3
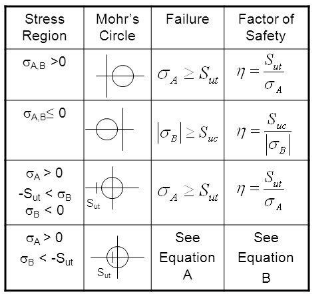
\:\text{Choose}\: \sigma_a \:\text{to be the largest stress}\: (\sigma_a = \sigma_1) \:\text{Choose}\: \sigma_b \:\text{to be the smallest stress}\: (\sigma_b = \sigma_3) For failure criteria:
\eta = \frac{\sigma_{ut}} {\sigma_a} \:\text{for Quadrant}\:\sigma_a\geq \sigma_b\geq 0\sigma_a\geq \sigma_b\geq 0\:\text{for Quadrant}\: \frac{\sigma_{a}} {S_{ut}} -\frac{\sigma_{b}} {S_{uc}} = \frac{1} {\eta} 0 \geq \sigma_a\geq sigma_b\:\text{for Quadrant}\: \eta = - \frac{S_{uc}} {\sigma_b} 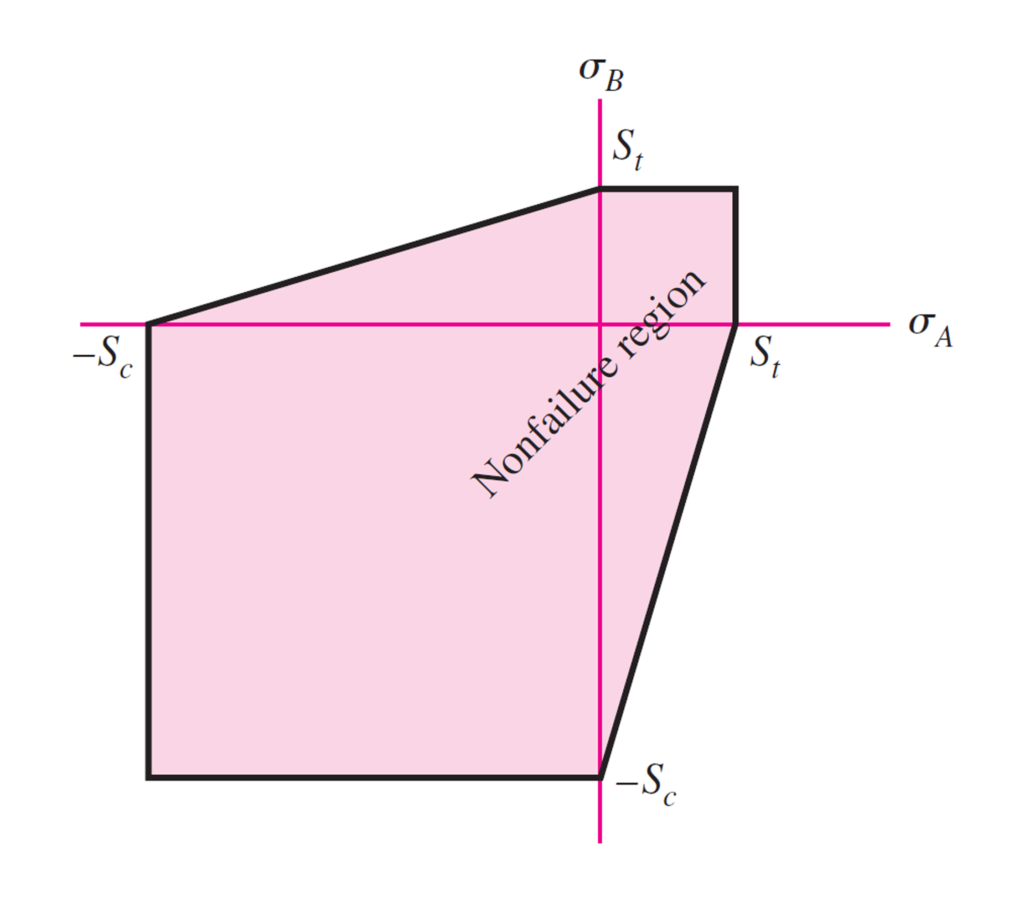
Although the Mohr-Coulomb criterion is widely used for isotropic brittle materials, some disadvantages limit its wider application for FEA structural analysis. One important disadvantage of this theory is ignoring the effect of the intermediate principal stress; it has an important influence on materials behavior. Therefore, Mohr-Coulomb’s theory is used only for materials in a biaxial state of stress.
Modified Mohr Theory:
Modified Mohr Theory, also known as the “Modified Coulomb-Mohr Theory,” is a modification of the original Coulomb-Mohr theory. It is the preferred theory for brittle materials.
This theory was originally developed to explain the behavior of rocks in tectonic settings. Now, however, it is also used to describe all materials that exhibit brittle behavior.
This theory provides a simple way to calculate strength in four quadrants. It makes it easier to predict behavior under stress.
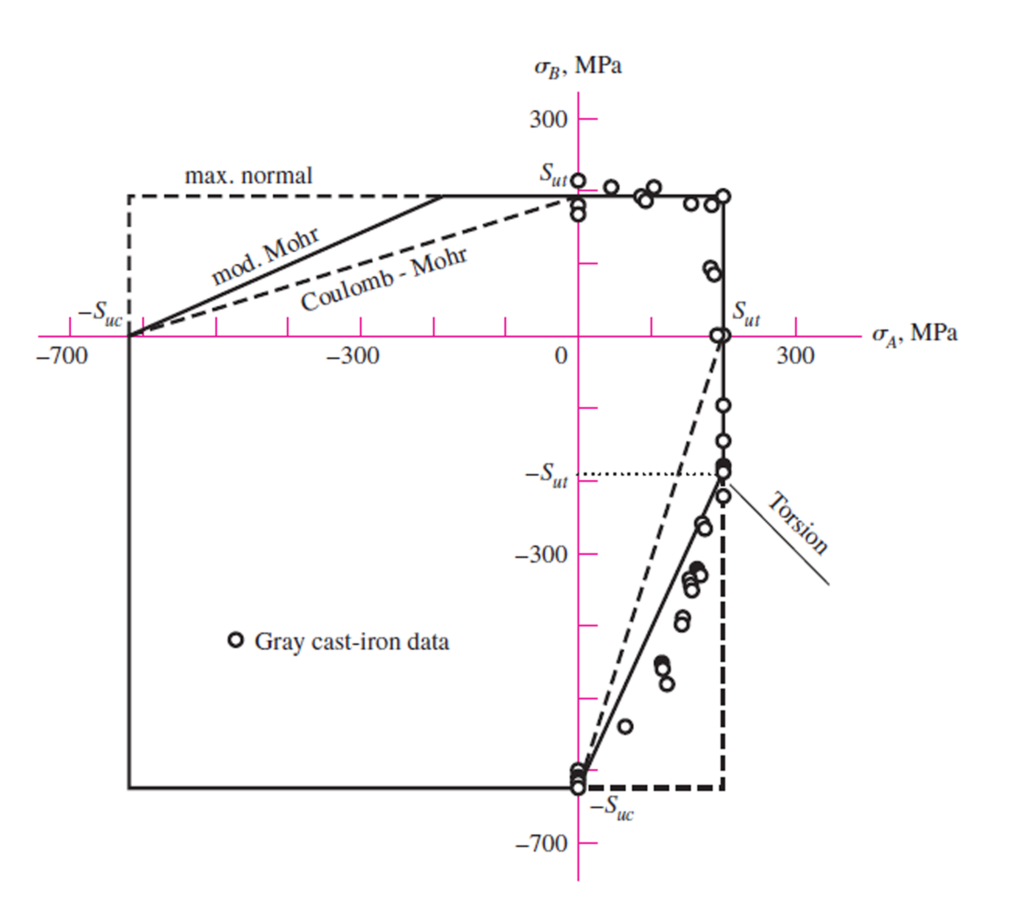
The problem with Coulomb-Mohr’s theory is that it tends to be conservative in the fourth quadrant. This can lead to overestimating your material’s strength at high confining pressures or low confining pressures.
This might not be bad if you’re trying to figure out what will happen under extreme conditions (like an earthquake), but it could lead you astray from what will actually happen during normal conditions.
Final Thoughts
We’ve continued our in-depth discussion by covering brittle materials failure analysis theory and mechanical stress terminologies. These included the Maximum Normal Stress Theory, the Mohr-Coulomb theory, and the Modified Mohr Theory.
A solid understanding of these three theories will allow you to predict failure during product development using FEA (Finite Element Analysis) in brittle materials. This is important knowledge as it affects many different fields.
For example, during the design process when engineers design a part or assembly for airplanes, trains, or any machine using FEA simulation, they want to ensure that the object won’t collapse from damage or be susceptible to extreme stress and strain on any portion of the structure.
We have shown that Maximum Normal Stress is inadequate because it is not accurate enough for safe structural analysis. Coulomb-Mohr is too conservative in the 4th quadrant, leading to over-design issues, which are costly and unnecessary.
Modified Mohr-Coulomb is the recommended analysis technique for brittle material failure and engineering fracture mechanics because it is slightly conservative in the fourth quadrant. Still, it has been determined that this behavior is more typical of brittle materials than other analysis techniques.